Optimizing Vibratory Screen Separator Performance
October 11, 2011
This article will demystify the set-up and operation of a round vibratory screen separator. The effect of the input control parameters: top weight force, bottom weight force, and lead angle are defined to create an understanding of vibration generation. The output parameter measurements techniques for: horizontal motion, vertical motion, and phase angle are defined to create an understanding of the vibration generated. This article will then explain the motion of particles inside the separator and how to adjust the weights to obtain the optimum vibratory motions. Practical guidelines are introduced for weight setting methodology to achieve optimum screening patterns.
Separator Basics
|
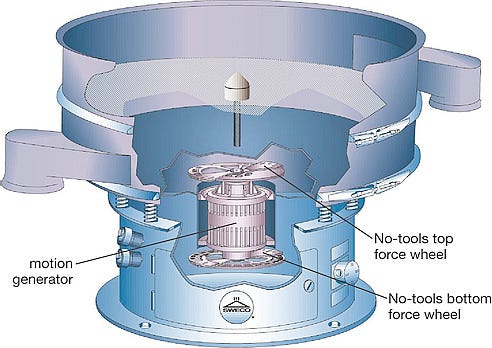
Figure 1: Sizing is the segregation of a variety of solid particles into separate groups containing comparable sizes. |
A standard round vibratory separator uses a vibrating screen cloth enclosed in frames that are vibrated by a motion generator consisting of a double-end shaft motor with eccentric weights on the top and bottom of the vertically mounted motor (see Figure 1). The motor rotates counter-clockwise (CCW) when viewed from the top. As the motor rotates, the weights generate a radial centrifugal force causing the spring mounted machine to vibrate.
The top weight has an adjustable force output and a fixed angular orientation on the motor shaft. The bottom weight also has an adjustable force output, but includes a variable angular orientation in relation to the top weight.
Adjusting Vibratory Motion
There are three independent variables or adjustments to a vibratory separator: top force, bottom force, and lead angle. The output variables are horizontal motion amplitude, vertical motion amplitude, and the phase angle. Lead angle is the angular weight setting while phase angle is the measured delay between the maximum vertical and horizontal amplitudes.
To simplify discussion, first consider only the top motor weight. The top motor eccentric weight is designed to be at the center of gravity (CG) of the vibrating machine. Force acting at the center of gravity of a mass will cause uniform planar motion in that mass. In other words, the top weight force spinning at the center of gravity will create a uniform horizontal radial motion of the machine without any torque about the CG.
|
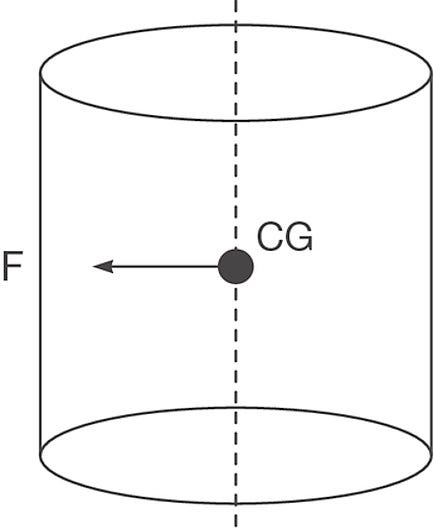
Figure 2. Separator’s center of gravity located amid the top eccentric weight force |
Visualize a separator as a solid cylinder as shown in Figure 2: The top eccentric weight force acts at the center of gravity (CG) of the body. When a force acts at the CG of the body, horizontal motion of the body will occur in the direction of the top weight force.
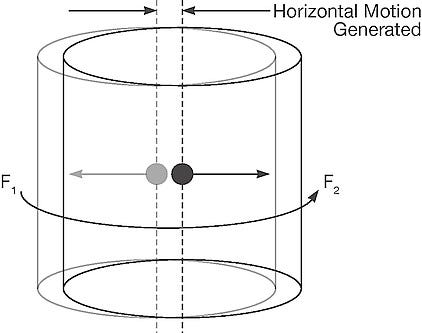
Figure 3 shows the same body at two different positions. The first position, shown in gray, occurs when the force is pointed left. As the motor rotates 180 degrees, the force will point to the right and cause the cylinder to translate horizontally to the right position shown in the black outline. The horizontal motion generated is the distance the separator moves with 180 degrees of motor rotation.
|
Figure 3: Seperator at two different positions on horizontal axis |
As the motor continuously spins the weights, we can visualize the cylinder moving through a horizontal radial motion following the eccentric weight force orbit. It is important to note that the cylinder does not rotate only the motor and weights. Because the top weight force acts at the center of gravity, the cylinder will always remain horizontal. Variable horizontal motions will occur as the magnitude of the top force is varied.
|
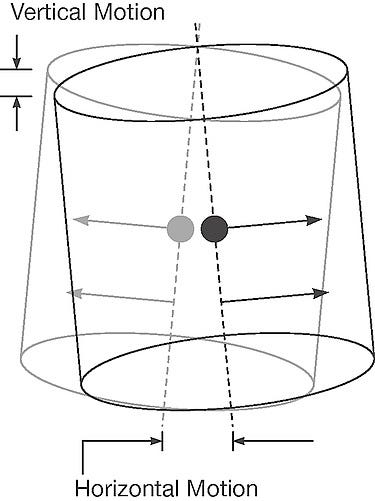
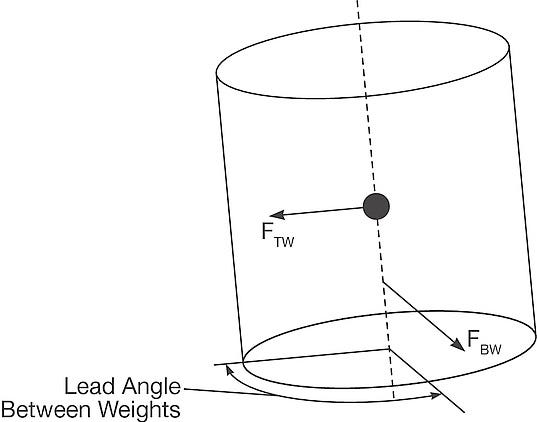
Figure 4: Bottom eccentric weight induces a torque to produce vertical motion |
Now, if we add a another eccentric weight FBW, as shown in Figure 4, to the bottom of the motor below the machine CG, the bottom eccentric weight will induce a torque about the center of gravity creating vertical motion as the machine tilts from the vertical axis. The result of the top and bottom weight is a cylinder tilted off the vertical axis. Adding more bottom weight yields more vertical motion.
|
Figure 5: Top and bottom force generate both horizontal and vertical motions |
Figure 5 depicts the same cylinder shown in Figure 4 in two different motor positions with the weights rotated 180 degrees. The drawing shows the resultant horizontal and vertical motions which are generated by the eccentric top and bottom weight forces.
We can visualize the motor rotating CCW and the maximum amplitude generated will occur in the direction the force points. As the motor rotates, the direction continually changes and the elliptical motion in three axes is generated by one rotation of the motor.
Figure 5 shows the top and bottom forces to be vertically aligned with the maximum horizontal and vertical motion occurring in the same vertical plane, or angular position. There are advantages to changing the angle between the weights.
In vibratory separators, lead angle is defined as the CCW angle between the top and bottom weight when viewed from above. When the weights are vertically aligned, there is a zero degree lead angle. When the bottom weight is 120 degrees CCW from the top weight, and the motor is spinning CCW, the bottom weight leads the top weight. This means the maximum vertical motion generated by the bottom weight will occur 120 degrees of motor rotation before the maximum horizontal motion generated by the top weight.
|
Figure 6: Lead angle determines the point at which maximum horizontal and vertical motion occur |
Figure 6 shows the bottom weight leading the top weight by 120 degrees. This figure also shows that the vertical and horizontal motion no longer occur at the same time.
Lead angle is the control parameter which gives a round vibratory separator unparalleled functionality by controlling the material flow pattern in the separator. The advantages and proper setting of lead angle will be discussed further in the particle dynamics section.
Measuring Vibration Amplitude
|
Figure 7: Vibration gauge sticker is used to measure both horizontal and vertical motion |
To analyze the motion of a separator, a vibration gauge sticker easily measures vibration amplitudes. These stickers are attached to the outside frame diameter of the machine near the screen level. The stationary gauge shown in Figure 7, measures both horizontal and vertical motion independently.
|
Figure 8: Amplitude is measured to the nearest 1/16 inch |
To read the vibration amplitude, while the machine is running, observe where the triangular lines cross as shown in Figure 8. The number closest to the line crossing will be the vibration amplitude in 1/16-in. increments. Figure 8 shows that the horizontal amplitude reads 3/16 and the vertical reads 3/16.
Motion amplitudes vary with the distance from the center of gravity of the machine. It is important when comparing machines that the measurements are in equivalent locations. It is best to measure amplitudes closest to the most critical screen in the separator.
If amplitude stickers are not available, use a felt tip marker to make a dot on the frame. A ruler can then be used to measure the horizontal and vertical amplitudes of the motion.
The next question is how to measure the phase angle between the horizontal and vertical motions. The simple answer is to merely reference the lead angle between the weights. While this is normally satisfactory, there are certain conditions where the lead angle does not predict the vibratory motion or the motion of particles on the screen. When lead angle is no longer appropriate, phase angle should be measured.
|
Figure 9: Motion analysis system electronically measures multiple system functions |
Phase angle is the measured delay between the maximum vertical and horizontal motion. A computer monitoring system is required for this measurement. Figure 9 shows a data screen from a computer based motion analysis system. Horizontal and vertical displacement, phase angle, motor speed, and directional accelerations allow precise set-up and troubleshooting of vibratory separators.
Particle Motion in Vibratory Separators
|
Figure 10: Material being fed onto the center of the screen |
Now that we understand the function of machine input parameters: top weight, bottom weight and lead angle, and the resulting separator motions, we can discuss how to control the motion of a particle. Figure 10 shows material feed onto the center of the screen moves from the center to the outside edge of the screen. Figure 11 shows material feed at the edge of the screen runs to the center of the screen. These material flow patterns can now be explained.
|
Figure 11: Material being fed at the edge of the screen |
The two key concepts of particle motion are:
1. The maximum vertical amplitude occurs directly above the bottom weight. This means that a particle on the screen will be launched vertically when the bottom weight rotates directly beneath that particle.
2. The maximum horizontal radial amplitude occurs in the direction of the top weight. As the top weight rotates towards a particle on the screen, the horizontal radial motion increases to a maximum when the top weight is pointed at the particle. As the weight rotates away from the particle, the horizontal radial motion decreases.
For the first example, analyze a machine set-up with the top and bottom weights at zero degree lead angle. Consider one particle on a screen directly above both of the weights. This particle will be launched vertically directly above the top and bottom weights at the position of maximum vertical and horizontal radial motion. While the particle is in flight above the screen, the weights will continue to rotate and move the screen underneath the flight of the particle. When the particle lands on the screen, it will be in a new position on the screen.
|
Figures 12: Particle motion is determined by machine parameters |
If we simply assume that a particle is in flight for 180 degrees of motor rotation with the weights set at a zero lead angle, the particle, depicted by the double-ended arrow in Figure 12, will leave the screen vertically and land closer to the screen edge. The 180-degree assumption clearly shows that the particle leaves the screen at the point of maximum horizontal radial motion, shown in gray outline, and lands at the point of minimum horizontal radial motion, shown in black. The particle will appear to travel radially outward from the screen center as shown in Figure 13.
|
Figures 13: Particle motion is determined by machine parameters |
With the weights set at zero degree lead angle, the particle will always travel radially outward even if the particle is in flight for only one degree of motor rotation. The particle left the screen at the point of maximum radial displacement and will land and a point of less radial displacement. This means the particle will always land closer to the edge of the screen.
For the second example, let us analyze the opposite extreme when the bottom weight is advanced to a 180-degree lead angle. Here the vertical motion occurs before the maximum horizontal radial motion; therefore, the particle will be launched vertically before the maximum radial motion occurs.
|
Figures 14: Particle motion is determined by machine parameters |
To continue the same analogy, let us again assume that the particle is in flight for 180 degrees of motor rotation, only now the lead angle is set to 180 degrees. The particle, depicted by the double-ended arrow in Figure 14, will leave the screen vertically above the bottom weight, be in flight above the screen for 180 degrees of motor rotation, and land again directly above the top weight. This is shown in Figure 14 with the particle leaving the screen shown in the gray outline and landing in the black outline screen position. When the particle left the screen, it was at the location of minimum horizontal radial displacement and landed at the location of the maximum radial displacement. The particle has landed farther from the outside edge of the screen and appears to travel radially inward as shown in Figure 15.
|
Figures 15: Particle motion is determined by machine parameters |
Again, using the same arguments, with the weights set at 180-degree lead angle, the particle will always travel radially inward even if the particle is in flight for one degree of motor rotation. This is because the flight of the particle begins when the separator is at the minimum horizontal radial distance. The particle left the screen at the point of minimum radial distance and will land and a point of greater radial distance.
Using these two extremes as examples, it is clearly shown how the lead angle is the controlling parameter in particle flow direction in a vibratory separator. The simplified discussions so far have been helpful to illustrate the effects of vibratory motion on particle motion, but realistically, particles are not in flight for 180 degrees of motor rotation.
|
Figures 16: Particle motion is determined by machine parameters |
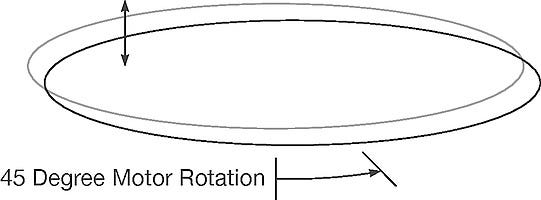
The past examples have ignored the second horizontal axis motion by only considering the 180-degree positions. When the motor has rotated 45 degrees, the screen position will have moved in two dimensions in the horizontal plane. Figure 16 shows the effect of 45 degrees of motor rotation. Figure 17 shows the top view of a single particle displacement on a screen. Figure 17 now clearly shows that a particle will more realistically move in two horizontal dimensions, with both radial and angular displacements.
|
0° Lead Angle |
|
15° Lead Angle |
|
35° Lead Angle |
|
90° Lead Angle |
Figure 18: The path particles travel across the screen is determined by the lead angle |
Figure 18 depicts the complete range of material flow patterns which can be obtained by adjusting the lead angle in a round vibratory separator.
As the lead angle is increased from zero degrees towards 50 degrees, the horizontal radial particle displacement is diminished. This means that the radial velocity of the particle will decrease because the horizontal tangential motion is increasing. This yields an increasing spiral path to the flow pattern.
At a 60-degree lead angle setting, the material appears to travel only tangentially. This can be explained by a particle being launched vertically 60 degrees before the top weight and landing 60 degrees after the top weight in the same radial position on the screen. Material will not readily discharge from the spouts at this setting.
As the lead angle increases above a 60 degree lead angle, the radial inward displacements increase. These patterns are explained simply by when the particle lands on the screen. If the particle lands after the maximum radial displacement, then the particle will move radially outward. If the particle lands before the maximum radial displacement, then the particle will move radially inward.
Summary
1. Top weight force controls the horizontal amplitude.
2. Bottom weight force controls the vertical amplitude.
3. Lead angle governs the material flow pattern and direction.
4. Horizontal and vertical amplitudes can be easily measured to evaluate and understand separator performance.
Greg Brock is a technical service representative who has been with Sweco (Florence, KY) for over 23 years with experience in several areas, including test facility management and engineering.
About the Author(s)
You May Also Like