High-accuracy feeders not only improve proportioning consistency but also create the opportunity to safely cut ingredient costs as well. By carefully exploiting a recipe's “ingredient tolerances,” processors can achieve significant material cost savings without compromising end-product quality. And with improved feeder accuracy, even greater savings can be realized.

Unlike the popular notion of a culinary recipe in which each step in the preparation of a dish is detailed, a process recipe primarily refers to the proportioning of the raw ingredients going into the finished product. Whether the end product is a snack food, a prescription drug, or a compounded plastic pellet, the process recipe to proportion the raw ingredients works roughly the same way. The proportioning system or feeder recipe controller must know the desired proportions, or percentages, of each ingredient in the recipe. As long as the feeding system can handle the ingredients and as long as it proportions them accurately enough, the result is generally acceptable, and the recipe stream is permitted to advance to the next processing operation.

However, things are changing. Armed with ever-sharper pencils, today's processors are hunting for more ways to trim costs. And since the cost of ingredients often comprises the lion's share of a product's total cost, processors are focusing more than ever on ways to achieve ingredients cost savings.

Making Room for Savings

According to traditional practice, once a recipe is defined, its costs are fixed. As long as a recipe conforms to its preestablished ingredient tolerances, any further improvement in proportioning performance has no effect on total ingredient cost. While more-accurate proportioning always increases a recipe's consistency, the total recipe cost remains unchanged because each ingredient remains at its originally targeted proportion. So where do savings possibilities lie?

Savings opportunities emerge by recognizing that ingredient tolerances are part of the recipe, not the proportioning system. A recipe's minimum/maximum ingredient tolerances simply specify the envelope within which each ingredient can be proportioned and still produce an acceptable result. These tolerances are specified to ensure that the resulting formulation will possess a predefined set of properties, attributes, or characteristics according to the processor's quality standards. Thus, the only practical constraint a recipe's tolerances place on the proportioning and feeding system is the imposition of a feeder performance minimum baseline for each ingredient.

In theory, a proportioning system whose performance is just accurate enough to operate within the recipe's prescribed tolerance boundaries is forced to position its operating setpoints at the midpoint of each ingredient's allowable range. Since more-accurate proportioning reduces ingredient variability, the feeder's variability range occupies less of the recipe's allowable tolerance range. As a result, the unused portion of preestablished tolerance allowances can be strategically exploited to reduce total ingredient costs. This cost-cutting concept is illustrated in Figure 1.

Figure 1b shows a sample recipe ingredient proportioned at an accuracy level just sufficient to avoid violating its associated tolerance limit. In this case, the operating setpoint must be positioned in the middle of the allowed range. However, as shown in Figure 1b, improved feeder accuracy narrows ingredient variability, freeing up a portion of its tolerance band. If an ingredient is relatively expensive, its proportion can be reduced, as shown in Figure 1c, without violating its tolerance limits. Similarly, if relatively inexpensive, an ingredient's proportion can be increased without violating tolerance limits, as demonstrated in Figure 1d.

Since total recipe proportions must always equal 100%, any reduction in the proportion of an expensive ingredient must be offset by an equal increase in the proportion of another ingredient. To minimize the total recipe cost, the most attractive choice is to assign the increase to the least expensive ingredient. When that is done, a net savings proportional to the difference in unit cost between the two ingredients is achieved. By repeating this procedure for all ingredients, total recipe costs can be minimized without violating any ingredient's tolerance allowance.

As demonstrated in the next section, as long as measured feed rate variability occupies less than the full tolerance range of two or more recipe ingredients, this strategy results in a recipe cost reduction even without an incremental improvement in feeder performance. However, improved feeder performance not only improves recipe consistency but also offers the potential to achieve ongoing ingredients savings.

The Minimization Method Detailed

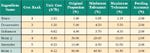
This approach is illustrated in Tables 1–3. Table 1 presents a hypothetical six-ingredient recipe. The quickest way to manually optimize a recipe is to work directly with each ingredient's range of possible operating setpoints. In Table 2, minimum (red) and maximum (blue) possible operating setpoints are calculated using the recipe's specified tolerance limits and by proportioning accuracies according to the formulas provided. If all ingredients are fed at their maximum possible operating setpoints, the sum of all ingredient proportions will exceed 100% (101.89% in this case—see the blue column titled Operating Max. %). However, by starting with this impossible recipe, its total can be reduced to the required 100% by progressively minimizing the proportions of relatively expensive ingredients.

The first step in this process is shown in the Minimize Rank 1 column in Table 2, in which only the most expensive ingredient is minimized and all other ingredients remain maximized. Since in this case the sum of all ingredients proportions still exceeds 100% (101.64%), an attempt can be made to minimize the next-most-expensive ingredient, the preservative, by replacing its maximum operating point with its minimum. The recipe in the Minimize Rank 2 column totals 100.85%, confirming that the Rank 2 ingredient can be fully minimized. In similar fashion, the enhancer (Rank 3) can also be fully minimized, producing a new recipe total of 100.42%. However, with only 0.42% to go before hitting the required 100% mark, it is apparent that the Rank 4 ingredient (Main 2) cannot be fully minimized. To restore the recipe to exactly 100%, Rank 4's proportion can only be reduced from its maximum by 0.42%, resulting in a final proportion of 29.97% and making it the lone recipe ingredient whose proportion is neither minimized nor maximized but placing it somewhere within its permitted range (shown in green). The Rank 5 and 6 ingredients, the least costly recipe components, remain maximized in the final cost-optimized solution.

As shown in Table 3, this solution results in a potential 2.15% recipe cost savings at the assumed tolerances and ingredient-feeding accuracies. A recalculation of the above recipe solution, assuming an improvement in proportioning precision to 1.0% versus the originally assumed 2.0% results in an additional 0.56% savings, or $27,280, amounting to a total annual savings of $133,720, or 2.71% of the total ingredient cost.

Achieving Savings Safely

A fully cost-minimized recipe solution represents the maximum possible savings available for a given application. For a variety of reasons, processors may feel uneasy about operating closer to tolerance limits than they are used to. Setting each ingredient's operating proportions midway between its tolerance limits provides the widest possible berth to accommodate any proportioning variation, regardless of its cause. However, as an optimized recipe's cost-cutting potential shows, such a safety margin carries the opportunity deficit of unrealized savings. Fortunately, there is a middle ground that is both practical and prudent.

Using the calculation technique detailed above, it is easy to generate any number of partially optimized recipe solutions in which any or all ingredients participate to whatever degree desired. With full control over a recipe's solution, processors can retain full confidence in their ability to reliably achieve the anticipated savings on the process line. It all has to do with the tolerance values one chooses to use.

While a recipe's quality assurance tolerances form the standard of formulation acceptability, strategically applying even more stringent tolerances enables the processor to customize the solution as required. For example, cautious but cost-conscious processors may wish to see whether problems arise if they optimize the recipe based on ingredient tolerances 50% tighter than called for in the original recipe. If no difficulties are encountered, they can try 25% in order to capture additional savings. Since all recipe solutions are based on proportioning system performance (i.e., feeder accuracy) in addition to recipe tolerances, further incremental savings become available when proportioning system performance is improved.

Any number of ingredients can be excluded from a partially or fully optimized recipe solution, as when the proportion of an ingredient must be held as closely as possible to a constant value. In that case, the ingredient feeder's repeatability is used to determine the effective tolerance limits in computing the optimized solution. For example, if a critical 1% recipe ingredient fed at an accuracy of 0.37% were to be excluded from the solution, its effective minimum/maximum tolerances would be entered as 0.9963% and 1.0037%, respectively. By using these feeder-derived tolerance values to calculate the optimized recipe solution, this ingredient's operating point would be constrained at its required 1% value.

Conclusion

Strategically manipulating ingredient operating points within a recipe's available tolerance ranges presents a potentially significant cost-savings opportunity. By minimizing the presence of expensive recipe components and maximizing the proportions of less-costly ingredients, processors can capture savings previously concealed within their recipe tolerance allowances. Any improvement in feeding accuracy leads to further improvements in ingredient cost savings and recipe uniformity.

John Winski is director of North and South America sales for K-Tron, Pitman, NJ. He has an associates degree in engineering from Temple University in Philadelphia and has been in the process industries and with K-Tron for 20 years. Winski can be reached at 856-256-3103 or [email protected]. For more information about K-Tron, visit www.ktron.com.